「順番による偏りを平均化して消すための実験デザインの工夫」です。
簡単な説明
実験で複数の条件をテストする際、条件の順序が結果に影響を与えることがあります。例えば、最初に実施した条件が参加者に新鮮で、その後の条件が疲労や慣れによって異なる結果を生む場合です。カウンターバランスは、こうした順序効果を除去するために条件の順序を変える方法です。
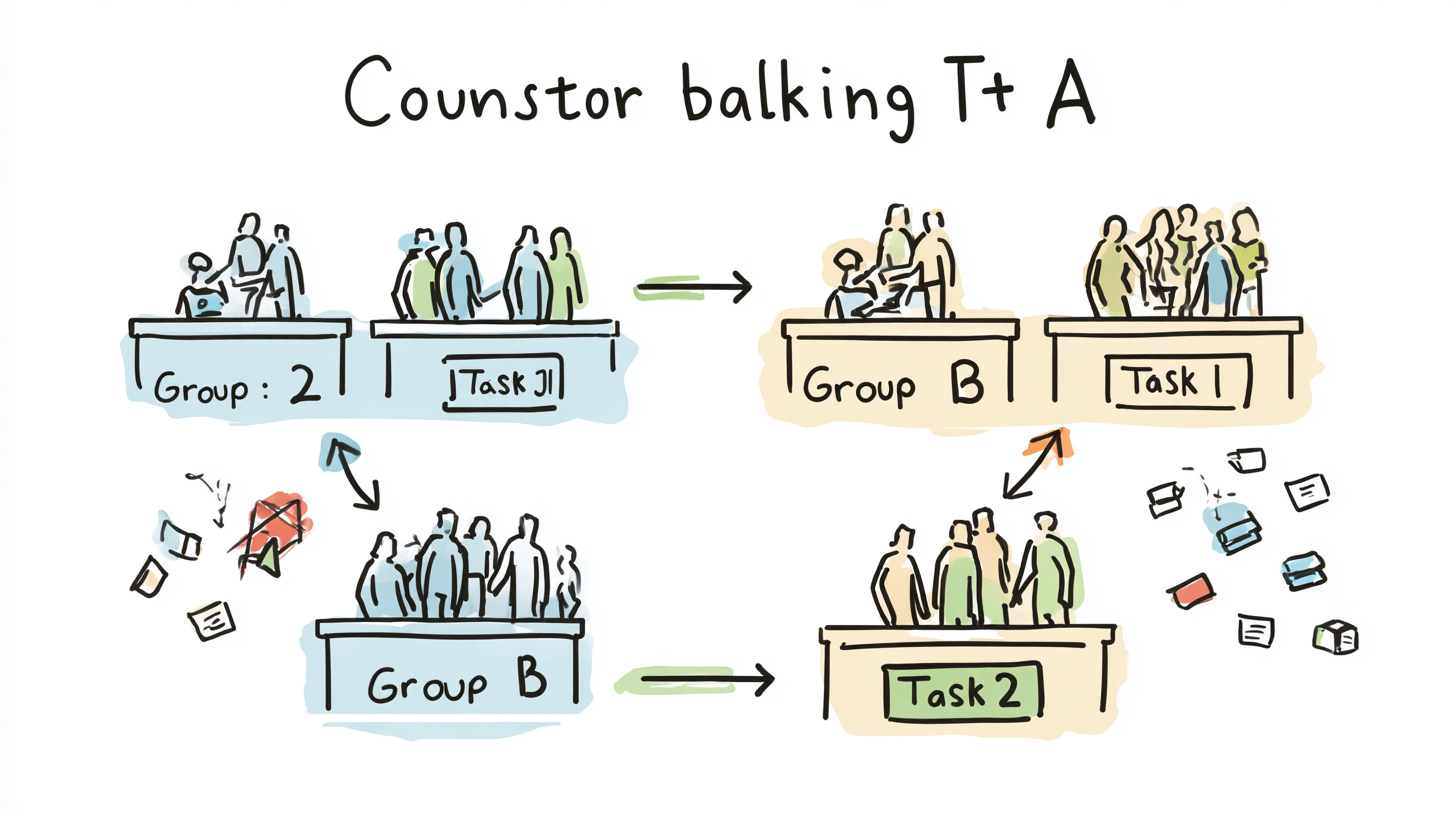
条件Aと条件Bをテストする実験を行うとき、すべての被験者に「A→B」の順で提示すると、Bの結果にAの影響が出るかもしれません。逆に、「B→A」にすれば今度はAが影響を受けるかもしれません。そこで、
- 半数の被験者には「A→B」
- 残りの半数には「B→A」
というように順序を交互に割り当てると、順序の影響が平均化されて、純粋な条件の違いだけが測定できます。
動画もありますので読むのが面倒な方はこちらをどうぞ
英語版はこちら
由来
心理学の実験では、刺激や課題の順番によって被験者の反応が変わってしまうことがあります(これを順序効果といいます)。
たとえば、難しい課題のあとに簡単な課題を出すと「簡単すぎて拍子抜け」したり、先に学んだ情報が後の課題に影響する(残存効果)こともあります。これを制御するために開発されたのが「カウンターバランス」という方法です。
カウンターバランスは、実験心理学や行動科学でよく使われる手法です。実験条件の順序が結果に与える影響を除去するために考案されました。順序効果(順序バイアス)は、参加者が複数の条件を異なる順序で経験することで結果が変わることを指します。これを防ぐために、条件の順序を様々に組み合わせるカウンターバランスが用いられます。
具体的な説明
カウンターバランスとは、実験において条件の順序が結果に影響を与えないようにするための手法です。例えば、A条件とB条件の二つの実験条件がある場合、参加者の半数にA条件を先に、B条件を後に実施し、残りの半数にB条件を先に、A条件を後に実施します。これにより、順序効果が平均化され、実験結果がより信頼性の高いものになります。
例えば、記憶実験でリストAとリストBを使用する場合、参加者の半分にリストAを先に記憶させ、その後リストBを記憶させる。残りの半分には逆の順序で実施する。結果として、どちらのリストが先に提示されたかに関わらず、リストの記憶性能が評価され、順序効果の影響が除去されます。
大学レベルでは、カウンターバランスは実験デザインの一部として詳しく学ばれます。特に、ラテン方格デザインやブロックランダム化といった高度なカウンターバランス手法が紹介されます。これらの手法は、複数の条件や多段階の実験において順序効果を最小限に抑えるために使用されます。
順序効果(Order Effect)は、実験の内部妥当性を脅かす要因のひとつです。
とくに**被験者内計画(within-subject design)**では、同じ参加者が複数の条件を経験するため、条件の順番が影響を与えるリスクがあります。
この影響を制御・平均化するためにカウンターバランスを用います。基本には全順列(完全カウンターバランス)を使用しますが、被験者数が順列の数に満たない場合は、部分カウンターバランス(ラテン方格法など)が使われます。
また、統計解析では「順序」を要因として分散分析に組み込むこともあります。
例文
「新しい学習方法の効果を比較する実験で、カウンターバランスを使用して、学習順序が結果に影響を与えないようにしました。」
疑問
- Qカウンターバランスとは何ですか?
- A
カウンターバランスとは、実験条件の順序が結果に影響を与えないようにするために、条件の順序を交互に入れ替える手法です。
- Qカウンターバランスを使用する目的は何ですか?
- A
カウンターバランスを使用する目的は、順序効果を除去し、実験結果の信頼性を高めることです。
- Qラテン方格デザインとは何ですか?
- A
ラテン方格デザインは、複数の条件が交互に提示されるように実験を設計する方法で、順序効果を最小限に抑えるために使用されます。
- Qカウンターバランスはどのような場合に使用されますか?
- A
カウンターバランスは、複数の実験条件をテストする際に、条件の順序が結果に影響を与える可能性がある場合に使用されます。
- Qカウンターバランスの具体例を教えてください。
- A
例えば、A条件とB条件をテストする際、参加者の半数にA→Bの順で実施し、残りの半数にB→Aの順で実施することで、順序効果を除去します。
- Q被験者が2人しかいないとき、カウンターバランスは使えますか?
- A
はい。1人にA→B、もう1人にB→Aとすれば、簡易なカウンターバランスになります。
理解度を確認する問題
カウンターバランスの主な目的は何ですか?
- 実験条件の数を増やす
- 順序効果を除去する
- 参加者の数を増やす
- データ収集の時間を短縮する
回答: 2. 順序効果を除去する
関連キーワード
- カウンターバランス
- 順序効果
- 実験デザイン
- ラテン方格デザイン
- ブロックランダム化
- 行動科学
- 順序バイアス
関連論文
Winer, B. J. (1991). Statistical Principles in Experimental Design. → 実験計画法においてカウンターバランスの重要性を解説。
Field, A. (2013). Discovering Statistics Using SPSS. → 被験者内デザインでの順序効果の統計的扱いを紹介。
覚え方
「順序を変えて結果を公平に、カウンターバランスで実験クリア!」というフレーズで、カウンターバランスの役割と重要性を覚えましょう。
「順番のせいで実験がブレるのはもったいないから、みんなで順番変えてバランス取ろうぜって話だよ!」






コメント